In geometry, “inverse” refers to an operation, transformation, or relationship that reverses the effect of another operation, bringing a figure or value back to its original state.
In simple words:
👉 If one geometric action changes something, its inverse undoes that change.
Inverse is one of those geometry terms that sounds intimidating at first but once you see it in action, it becomes surprisingly logical and even fun. Whether you’re a student revising math, a teacher explaining transformations, or just someone curious about geometric concepts, understanding inverse in geometry will instantly sharpen your problem-solving skills.
Let’s break it down step by step, using plain language, real examples, and visual-friendly explanations no math anxiety required 😊
📐 Why “Inverse” Matters in Geometry
Inverse concepts appear everywhere in geometry from transformations and functions to angles, ratios, and coordinate geometry. Once you understand inverses, you can:
- Check your answers for accuracy
- Reverse transformations step-by-step
- Understand symmetry and balance in shapes
- Solve problems faster and more confidently
Inverse geometry isn’t just theory it’s a power tool.
📚 Origin of the Term “Inverse”
The word inverse comes from the Latin invertere, meaning “to turn upside down” or “to reverse.”
How it entered mathematics:
- Adopted in early European mathematics (16th–17th century)
- First widely used in algebra and geometry to describe opposite operations
- Later expanded into transformations, trigonometry, and coordinate geometry
Today, inverse is a core mathematical term taught globally.
🔁 What Does Inverse Mean in Geometry?
In geometry, something is inverse if it undoes or reverses the effect of something else.
Think of it like this:
- Forward action → changes the shape
- Inverse action → restores the original shape
Everyday analogy:
- Wearing shoes 👟 = action
- Taking shoes off = inverse action
Same logic applies in geometry.
🔺 Common Types of Inverse Concepts in Geometry
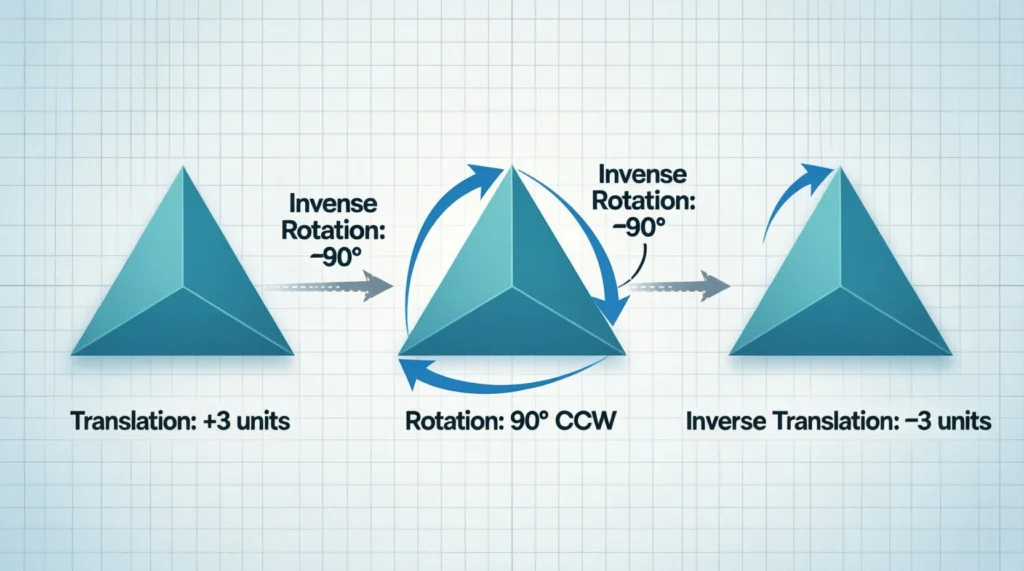
1️⃣ Inverse Transformations (Most Common)
Transformations move or change shapes. Their inverses reverse those movements.
Examples:
- Translation ↔ Translation in opposite direction
- Rotation ↔ Rotation by same angle in opposite direction
- Reflection ↔ Reflection over the same line
- Dilation ↔ Dilation using reciprocal scale factor
🔍 Example Table: Transformations and Their Inverses
| Transformation | What It Does | Inverse Transformation |
|---|---|---|
| Translation | Slides a shape | Slide back same distance |
| Rotation | Turns a shape | Rotate opposite direction |
| Reflection | Flips a shape | Reflect again over same line |
| Dilation (×2) | Enlarges shape | Dilation (×½) |
📌 Key rule: Applying a transformation and then its inverse gives you the original figure.
2️⃣ Inverse Operations in Geometry
Geometric calculations often involve operations and each has an inverse.
| Operation | Inverse |
|---|---|
| Addition | Subtraction |
| Multiplication | Division |
| Squaring | Square root |
Example:
If the area of a square is found by squaring the side length,
👉 the inverse operation helps you find the side length from the area.
3️⃣ Inverse Functions (Coordinate Geometry)
In coordinate geometry, inverse functions swap x and y values.
Example:
- Original function:
y = 2x + 3 - Inverse function:
x = 2y + 3→ solved fory
📍 Graphically, inverse functions reflect over the line y = x.
4️⃣ Inverse Relationships in Geometry
Some geometric relationships are inverse by nature.
Examples:
- As radius increases, curvature decreases
- As scale factor increases, detail decreases
- Larger denominator → smaller fraction (inverse proportionality)
🧠 Real-World Usage of Inverse Geometry
Inverse geometry isn’t just classroom math it’s used in real life.
📐 Architecture & Engineering
- Reversing transformations in blueprints
- Scaling models up and down accurately
🎮 Computer Graphics & Animation
- Undoing rotations and translations
- Camera movement reversal
🛰️ Navigation & Mapping
- Converting coordinates back to original positions
- Satellite imaging corrections
🧩 Problem Solving
- Checking geometric proofs
- Verifying symmetry and balance
🧪 Geometry Examples with Context & Tone
✔ Friendly / Neutral Example
“If you rotate the triangle 90° clockwise, the inverse is rotating it 90° counterclockwise.”
📘 Academic / Professional Example
“The inverse transformation restores the figure to its original orientation.”
❌ Negative / Dismissive Example (Rare but Possible)
“That solution ignores the inverse transformation, making the result incorrect.”
😄 Emojis are rarely used in formal geometry—but in learning contexts, they help!
🔄 Comparison: Inverse vs Related Geometry Terms
| Term | Meaning | How It’s Different |
|---|---|---|
| Inverse | Reverses an operation | Undoes effect |
| Opposite | Completely different direction | Not always reversible |
| Reciprocal | Multiplicative inverse | Only applies to numbers |
| Complement | Adds up to 90° | Angle-specific |
| Supplement | Adds up to 180° | Angle-specific |
🧭 Alternate Meanings of “Inverse”
While geometry focuses on reversal of transformations, inverse can mean:
- Algebra: Reversing a function
- Trigonometry: Inverse trig functions (sin⁻¹, cos⁻¹)
- Physics: Inverse-square law
📌 In geometry, the meaning is visual and spatial, not just numerical.
✨ Polite or Professional Alternatives to “Inverse”
In formal writing or explanations, you may also see:
- Reverse transformation
- Opposite operation
- Undoing the transformation
- Reciprocal process (when applicable)
These are useful when simplifying explanations for beginners.
❓ FAQs
1. What does inverse mean in geometry in simple words?
It means an action that undoes another geometric action.
2. What is an inverse transformation?
A transformation that returns a figure to its original position or size.
3. Is reflection its own inverse?
Yes. Reflecting a shape twice over the same line returns it to its original form.
4. What is the inverse of a rotation?
A rotation of the same angle but in the opposite direction.
5. Are inverse functions part of geometry?
Yes, especially in coordinate geometry and graphing.
6. What is the inverse of dilation?
A dilation using the reciprocal of the scale factor.
7. Why are inverses important in geometry?
They help verify solutions, reverse transformations, and understand symmetry.
8. Is inverse the same as opposite?
Not always. Inverse specifically reverses an operation, while opposite may not restore the original state.
📌 Conclusion
It means undoing, reversing, or restoring a simple idea with powerful applications. From basic transformations to advanced coordinate geometry, inverse concepts help bring balance, accuracy, and clarity to geometric thinking. Once you master inverses, geometry stops feeling like memorization and starts feeling like logic.
And that’s where math becomes satisfying ✨

Alex Ferguson is a word enthusiast at ValneTix.com who turns the meanings of everyday words into fascinating discoveries. His articles make learning language easy, enjoyable and practical for all readers.